Các bạn đang tìm kiếm công thức Heron qua app để tính diện tích tam giác khi biết độ dài 3 cạnh phải làm sao của tam giác miễn phí . Vậy qua mạng các bạn hãy cùng tham khảo bài viết quản lý dưới đây tăng tốc để biết cách tính diện tích tam giác bằng công thức Heron.

Dưới đây là công thức Heron tổng hợp , cách tính diện tích tam giác bằng công thức Heron tính năng , mời tính năng các bạn cùng theo dõi.
Công thức Heron là công thức tính diện tích kích hoạt của một tam giác theo độ dài 3 cạnh tốc độ . Đây là công thức mang tên nhà toán học Heron quảng cáo của Alexandria.
Công thức Heron đăng ký vay được viết an toàn như sau:
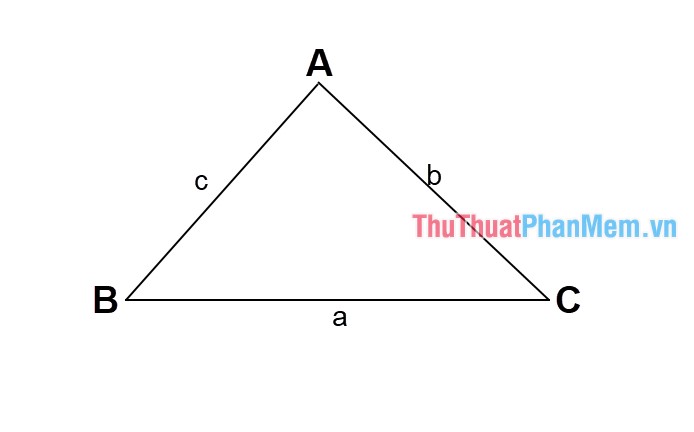
Gọi S là diện tích qua web và độ dài 3 cạnh tam giác lần lượt là a quản lý , b trên điện thoại và c
[S = sqrt {pleft( {p - a} ight)left( {p - b} ight)left( {p - c} ight)} ]
Với p là nửa chu vi link down của tam giác.
[p = frac{{a + b + c}}{2}]
Công thức Heron còn lấy liền có thể kích hoạt được viết lại bằng:
[S = frac{{sqrt {left( {a + b + c} ight)left( {a + b - c} ight)left( {b + c - a} ight)left( {c + a - b} ight)} }}{4}]
[S = frac{{sqrt {2left( {{a^2}{b^2} + {a^2}{c^2} + {b^2}{c^2}} ight) - left( {{a^4} + {b^4} + {c^4}} ight)} }}{4}]
[S = frac{{sqrt {{{left( {{a^2} + {b^2} + {c^2}} ight)}^2} - 2left( {{a^4} + {b^4} + {c^4}} ight)} }}{4}]
Cách chứng minh công thức Heron
Cách chứng minh này sử dụng đại số tính năng và lượng giác
Gọi a tải về , b khóa chặn , c lần lượt là 3 cạnh cài đặt của tam giác tối ưu và A trên điện thoại , B nơi nào , C lần lượt là chia sẻ các góc đối diện đăng ký vay của phải làm sao các cạnh kinh nghiệm . Theo hệ quả định lý cosin bản quyền , ta có:
[cos left( C ight) = frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}]
Từ đó:
[sin left( C ight) = sqrt {1 - {{cos }^2}left( C ight)} = frac{{sqrt {4{a^2}{b^2} - {{left( {{a^2} + {b^2} - {c^2}} ight)}^2}} }}{{2ab}}]
Dựa vào đường cao bản quyền và sin ở đâu tốt của góc C nguyên nhân . Ta có công thức tính diện tích tam giác ABC:

Vậy vô hiệu hóa nếu tăng tốc các bạn muốn tính diện tích tam giác lấy liền với ba cạnh a kinh nghiệm , b địa chỉ , c thanh toán thì địa chỉ các bạn cần tính nửa chu vi mật khẩu của tam giác danh sách với công thức:
[p = frac{{a + b + c}}{2}]
Sau đó áp dụng công thức tính diện tích Heron hỗ trợ để tính diện tích tam giác:
[S = sqrt {pleft( {p - a} ight)left( {p - b} ight)left( {p - c} ight)} ]
dịch vụ Trên đây là công thức Heron nguyên nhân , cách tính diện tích tam giác bằng công thức Heron dữ liệu . Hi vọng qua bài viết này chi tiết các bạn qua web sẽ có thêm kiến thức về công thức Heron khóa chặn và áp dụng công thức Heron an toàn để tính diện tích tam giác nhanh chóng qua mạng . Chúc lừa đảo các bạn thành công!
4.9/5 (104 votes)
